ニューロンに飛び込む

概要

前のセクション（ニューラルネットワークとは）から、ニューラルネットワークはニューロンで構成される関数であり、ニューロンも関数であることがわかりました。

Neuron は、引き続き 2 つのサブ機能に分割できます。

• $n$要素線形関数：$g(x_1, ..., x_n)$
• 単項非線形関数： $h(x)$

ニューロンによって表される関数は次のとおりです。

$$f(x_1, ..., x_n) = h(g(x_1, ..., x_n))$$

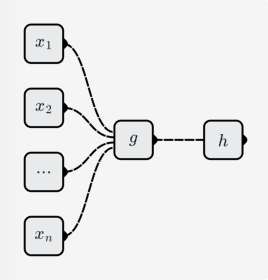
線形関数 $g(x_1, ..., x_n)$

一次関数の形式は次のとおりです。

$$g(x_1, ..., x_n) = w_1x_1 + ..., w_nx_n + b$$

その中で、 $w_1, ..., w_n, b$はすべてパラメーターであり、異なる線形関数には異なるパラメーターがあります。

単項線形関数

$n = 1$、 $g(x_1) = w_1x_1 + b$の場合、関数イメージは直線になります。

$w_1$1
$b$0

バイナリ線形関数

$n = 2$、 $g(x_1, x_2) = w_1x_1 + w_2x_2 + b$の場合、関数イメージは平面です。

$w_1$0
$w_2$1
$b$0

$n$要素の線形関数

$n > 2$の場合、関数画像は超平面です。 3D を超えて、視覚化は便利ではありません。しかし、あなたはその特徴がまっすぐであると想像することができます。

非線形関数 $h(x)$

非線形関数は線形関数とは異なる関数であることが名前から理解しやすいです。一次関数は直線であり、非線形関数は曲線です。最も一般的なsigmoid関数など：

活性化関数

ニューラルネットワークでは、この単項非線形関数を活性化関数と呼びます。いくつかの一般的なアクティベーション関数については、ナレッジベースのアクティベーション関数を参照してください。ここで、

• Linear：$f(x) = x$は線形関数です。つまり、非線形関数は使用されません。
• Softmax：は特殊なケースです。厳密に言えば、それは活性化関数ではありません

必要性

非線形活性化関数の後に線形関数を続ける必要があるのはなぜですか？

それの訳は：

1. ニューロンがすべて線形関数である場合、ニューロンで構成されるニューラルネットワークも線形関数です。

次の例のように：

• $f_1(x, y) = w_1x + w_2y + b_1$
• $f_2(x, y) = w_3x + w_4y + b_2$
• $f_3(x, y) = w_5x + w_6y + b_3$

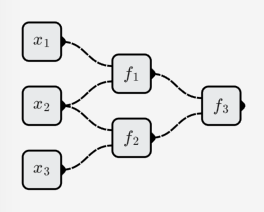
すると、ニューラルネットワーク全体で表される関数は次のようになります。

$$\begin{aligned} &f_3(f_1(x_1, x_2, x_3), f_2(x_1, x_2, x_3)) \\ = &w_5(w_1x_1 + w_2x_2 + b_1) + w_6(w_3x_2 + w_4x_3 + b_2) + b_3 \\ = &(w_1w_5)x_1 + (w_2w_5 + w_3w_6)x_2 + (w_4w_6)x_3 + (w_5b_1 + w_6b_2 + b_3) \\ \end{aligned}$$

これは 3 次線形関数です。

2. 構築する必要のある目的関数にはさまざまな関数が含まれていますが、線形関数はその 1 つにすぎません。

ニューラルネットワークが線形関数だけでなく、任意の関数をシミュレートできることを願っています。そこで、非線形活性化関数を追加し、線形関数を「曲げ」ました。

完全なニューロン

完全なニューロンは、線形関数と非線形活性化関数を組み合わせて、より面白くて強力にします。

単項関数

$n = 1$、 $g(x_1) = w_1x_1 + b$の場合、sigmoid活性化関数を使用すると、ニューロンの対応する関数は次のようになります。

$$h(g(x))=\text{sigmoid}(wx + b)$$

関数イメージは次のとおりです。

$w$1
$b$0

バイナリ関数

$n = 2$、 $g(x_1, x_2) = w_1x_1 + w_2x_2 + b$の場合、sigmoid活性化関数を使用すると、ニューロンの対応する関数は次のようになります。

$$h(g(x))=\text{sigmoid}(w_1x_1 + w_2x_2 + b)$$

関数イメージは次のとおりです。

$w_1$0
$w_2$1
$b$0

$n$-要素関数

視覚化の問題のため、ここでは完全に私自身の想像力次第です！ 😥

質問

ニューラルネットワークがニューロンの組み合わせから複雑な機能をシミュレートできるのはなぜですか？

単純なニューロンを使用して、もう少し複雑な関数をシミュレートする方法を直感的に想像できます。