Neural Network

日本語

ニューラルネットワークとは
1. ニューロンに飛び込む
2. ニューラルネットワークはどのように任意の関数をシミュレートしますか
3. なぜニューラルネットワークが必要なのですか
ニューラルネットワークの構築方法
1. 完全に接続されたニューラルネットワーク
2. グラフィカルツールを使用してニューラルネットワークを設計する
3. 出力層の「活性化関数」
ニューラルネットワークをトレーニングする方法
1. 学習アルゴリズムと原理
2. ニューラルネットワークをゼロから構築してトレーニングする
3. PyTorchを使用してコードを書き直します
4. グラフィカルツールを使用してニューラルネットワークをトレーニングする
ニューラルネットワークのいくつかの重要な問題
1. ネットワーク構造
2. 過剰適合
3. アンダーフィッティング
4. 過剰適合と過適合
5. 初期化
6. 勾配消失と爆発勾配
畳み込みニューラルネットワーク（CNN）
1. 1D畳み込み
2. 1D畳み込み実験
3. 1D-pooling
4. 1D-CNN実験
5. 2D-CNN
6. 2D-CNN実験
リカレントニューラルネットワーク（RNN）
1. バニラRNN
2. Seq2seq, Autoencoder, Encoder-Decoder
3. 高度なRNN
4. RNN分類実験
自然言語処理
1. Embedding: 記号を値に変換する
2. テキスト分類1
3. テキスト分類2
4. TextCNN
5. エンティティの認識
6. 単語のセグメンテーション、品詞のタグ付け、チャンク
7. 実行中のシーケンスタグ付け
8. 双方向RNN
9. BI-LSTM-CRF
10. 注意
言語モデル
1. n-gramモデル: 単語
2. n-gramモデル: 2-gram
3. n-gramモデル: 3-gram
4. RNN言語モデル
5. Transformer言語モデル
線形代数
1. ベクター
2. マトリックス
3. 行列の乗算に飛び込む
4. テンソル

ニューラルネットワークとは

概要

要するに、ニューラルネットワークは機能です：入力データ、出力結果。

関数

対応する関数形式を定義する例として、MNIST 手書き数字画像認識を取り上げましょう。

タスクタイプ：画像分類
入力：画像には 28 x 28 = 784 ピクセルが含まれ、各ピクセルは実数で表されます
出力:0-9
タスクの説明：画像から一意の番号を特定します
関数の定義

\begin{aligned} y &= f(x_1, x_2, ..., x_{784}) \\ &x_i \in \mathbb R, i = 1, ..., 784 \\ &y \in \{0, 1, ..., 9\} \end{aligned}

これはニューラルネットワークのエントリーレベルのアプリケーションです。入力は、784 個の入力変数を持つ関数に対応する低解像度（28 x 28）のグレースケール画像です。メガピクセルのカラー画像の場合、対応する入力変数は 300 万に達します。

ニューラルネットワークはいくつかの複雑な問題を解決するために使用されており、対応する機能も複雑であることがわかります。アルゴリズムの実現は、対応する関数を構築することです。

このような複雑な関数をどのように構築するのですか？簡単な関数から始めることができます。最も単純で最も成功した例はデジタル回路です。

デジタル回路

デジタル回路はコンピューターの基礎であり、私たちの巨大なデジタル世界を構築してきました。ただし、そのコアは AND, OR、および NOT 論理ゲートで構成されています。

論理ゲートとは何ですか？それは実際には関数です。そして、それらは最も単純な関数です。

論理ゲート	式	関数形式
ANDゲート	$x \land y$	$z = \land(x, y)$
ORゲート	$x \lor y$	$z = \lor(x, y)$
NOTゲート	$\lnot x$	$y = \lnot(x)$

変数タイプ：すべてのブール変数、2 つの値のみ： $\{T, F\}$ 、自然数（ $\mathbb N$ ）および実数（ $\mathbb R$ ）。
変数の数：単項関数または二項関数。これは関数の最も単純な形式でもあります。
関数表現：説明には真理値表を使用します。画像を使ってみませんか？離散関数であるため、画像上に孤立点がいくつかあり、あまり魅力的ではありません。

NOTゲート

$x$	$\lnot x$
$T$	$F$
$F$	$T$

NOTゲートイメージ（ $F$ には0を使用し、 $T$ には 1 を使用）

ANDゲート、ORゲート

$x$	$y$	$x \land y$	$x \lor y$
$T$	$T$	$T$	$T$
$T$	$F$	$F$	$T$
$F$	$T$	$F$	$T$
$F$	$F$	$F$	$F$

ANDゲート画像

ORゲート画像

組み合わせ論理ゲート

単純な論理ゲートを組み合わせて、より強力な機能を取得します。

新しいバイナリ関数を作成します。

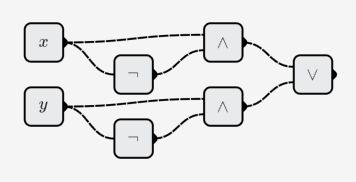
XOR: $x \oplus y = (x \land \lnot y) \lor (\lnot x \land y)$

XNOR: $x \odot y = (x \land y) \lor (\lnot x \land \lnot y)$

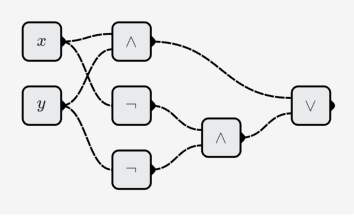
多変量関数を作成します。

3 ビット AND 演算： $f(x, y, z) = x \land y \land z$

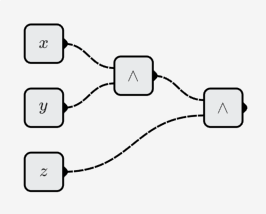
8 ビット加算器： $f(x_1, ..., x_8, y_1, ..., y_8)$ $f (x_{1}, ..., x_{8}, y_{1}, ..., y_{8})$
- 16 個のブール変数を含む 16 要素の関数です
32 ビット加算器： $f(x*1, ..., x*{32}, y*1, ..., y*{32})$ $f (x * 1, ..., x * 32, y * 1, ..., y * 32)$
- これは、64 個のブール変数を含む 64 要素の関数です。
- これは、32 ビット整数の 2 進関数と見なすこともできます： $f(x, y) \quad x, y \in \text{Int32}$

要約

単純な論理ゲート機能を組み合わせることにより、新しい論理機能を構築することができます。 32 ビット整数の加算、減算、乗算、除算などの演算、および 32 ビット単精度浮動小数点型の演算などが含まれます。

プログラミング言語

プログラミング言語をもう一度見てみましょう。例として Python を取り上げ、Python の要素を見てください。

演算子

名前	シンボル	関数
論理演算子	and or not	バイナリおよび単項論理関数
算術演算子	+、-、、/、％、*、//	二変数
比較演算子	==、！=、>、<、>=、<=	二変数
...

浮動小数点数の加算演算子（+）を例にとると、関数イメージは次のようになります。

$f(x, y) = x + y$

関数

Python で独自の関数を定義できます。

def f(x, y):
    return max(0, 2*x + 3*y - 3)

ここで新しい関数が定義されています。「+、-、*、max」などの関数を使用して、新しい関数を作成します。構築方法も関数の合成を介して行われます。

要約

関数はプログラミング言語のいたるところにあります。基本的な機能を組み合わせることで、新しい機能を構築し、新しいアルゴリズムを得ることができます。

神経網

ニューラルネットワークも機能しています。デジタル回路やプログラミング言語と同様に、単純な関数で構成されています。デジタル回路の基本単位は、AND, OR, NOT などの論理関数です。プログラミング言語の基本単位はさまざまな演算子などの関数ですが、ニューラルネットワークの基本単位はニューロンです。

ニューロン

では、ニューロンとは何ですか？生物学的ニューロンは、入力樹状突起と出力軸索を持つ細胞です。そして、ニューラルネットワーク上のニューロンは人工ニューロンであり、機能でもあります。より正確には、一種の機能です。

ニューロンの入力数は変更できます。つまり、これは $n$ 要素関数 $f(x_1, ..., x_n)$ を表し、 $n$ は異なる場合があります。ニューロン。

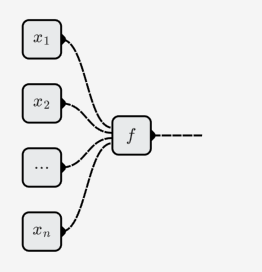
神経網

ニューロンは互いに結合してニューラルネットワークを形成します。以下に示すように：

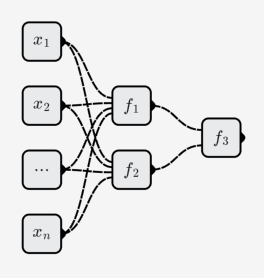
ニューラルネットワークには 3 つのニューロンが含まれています（入力ニューロンはカウントしないでください）。

$f_1(x_1, ..., x_n)$
$f_2(x_1, ..., x_n)$
$f_3(x_1, x_2)$

ニューラルネットワークによって表される関数は次のとおりです。

f(x_1, ..., x_n) = f_3(f_1(x_1, ..., x_n), f_2(x_1, ..., x_n))

要約する

デジタル回路（ハードウェア）の中核は機能であり、その基本的な機能は AND ORNOT 論理ゲート機能です。
プログラミング言語（ソフトウェア）の中核は関数であり、その基本的な関数は、さまざまな演算子関数と組み込み関数（ハードウェアまたは複合関数によって提供される）です。
ニューラルネットワークの中核も機能であり、その基本的な機能はニューロンです。
単純な関数を構成することにより、新しい関数を構築できます。ニューラルネットワークは、ニューロンの機能から関数合成操作によって構築された関数です。

質問

ニューロンによって表される関数は正確には何ですか？

それが $n$ 要素関数であることを知っているだけでは十分ではありません。デジタル回路の基本単位 AND, OR、および NOT ゲートはすべて真理値表をリストし、図を描きますが、ニューロンはどうですか？