ニューラルネットワークはどのように任意の関数をシミュレートしますか

概要

ニューラルネットワークが強力である理由は、その強力なシミュレーション能力にあります。理論的には、無限に小さなエラーで任意の関数をシミュレートできます。

言い換えれば、ニューラルネットワークを使用して任意の関数を構築し、任意のアルゴリズムを取得できます。

ここでは、直感的な理解を得るために、いくつかの視覚的な例を使用します。

単項関数のシミュレーション

直線

これは最も単純なケースであり、活性化関数のないニューロンを使用してシミュレートできます。

$$f(x) = wx + b$$

$w$1
$b$0

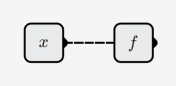
$w, b$パラメータを調整することにより、任意の直線をシミュレートできます。

ステップ関数

sigmoid活性化関数を持つニューロンを使用してシミュレートします。

$w$30
$b$0

$w$パラメータが増加し続けると、ニューラルネットワークは徐々に関数に近づきます。

矩形パルス関数

それをいくつかのステップに分けます。

1. 単一のニューロンを使用して、関数の左半分をシミュレートします。

$$f_1(x) = \text{sigmoid}(w_1x+b_1)$$

$w_1$20
$b_1$20

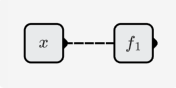
2. 単一のニューロンを使用して、関数の右半分を（逆さまに）シミュレートします。

$$f_2(x) = \text{sigmoid}(w_2x+b_2)$$

$w_2$20
$b_2$-20

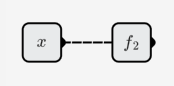
3. 別のニューロンを使用して、最初の 2 つのステップの画像を合成します

$$f_3(x, y) = \text{sigmoid}(w_{31}x + w_{32}y + b_3)$$

$w_{31}$10
$w_{32}$-10
$b_3$-5

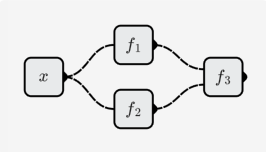
得られた結果は、目的関数の適切な近似です。

その他の単項関数

長方形のインパルス関数を使用すると、積分の原理と同じように、他の任意の関数を簡単に近似できます。

$n$10

実験

Broken Lineミッションを完了し、各ニューロンに対応する関数を観察します。

二関数のシミュレーション

飛行機

これは最も単純なケースであり、活性化関数のないニューロンを使用してシミュレートできます。

$$f(x, y) = w_1x + w_2y + b$$

$w_1$0
$w_2$1
$b$0

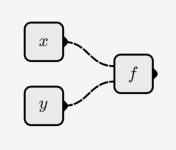
$w_1, w_2, b$のパラメータを調整することにより、任意の平面をシミュレートできます。

バイナリステップ関数

sigmoid活性化関数を持つニューロンを使用してシミュレートします。

$$f(x) = \text{sigmoid}(w_1x + w_2y + b)$$

$w_1$0
$w_2$30
$b$0

バイナリ矩形インパルス関数

単項関数の場合と同様に、段階的に実装します。

1. 単一のニューロンを使用して、関数のエッジをシミュレートします

$$f_1(x, y) = \text{sigmoid}(w_{11}x + w_{12}y + b_1)$$

$w_{11}$0
$w_{12}$20
$b_1$20

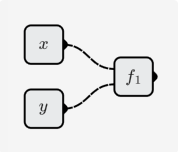
2. 次に、次の関数を取得できます。

$w_i$10
$w_j$-10
$b_i$-5

3. 最後に、次の関数を合成できます

$w_{51}$10
$w_{52}$-10
$w_{53}$10
$w_{54}$-10
$b_5$-15

最終的なニューラルネットワーク構造を次の図に示します。

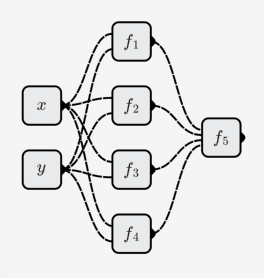
その他のバイナリ関数

バイナリ矩形インパルス関数を使用すると、積分の原理と同じように、他のバイナリ関数を簡単に近似できます。

実験

Circleミッションを完了し、各ニューロンに対応する機能を観察します。

n 要素関数のシミュレーション

原理は同じです、あなた自身のために想像してください！ 😥

質問

すでにデジタル回路とソフトウェアプログラムアルゴリズムがありますが、なぜニューラルネットワークが必要なのですか？

デジタル回路上に構築されたソフトウェアプログラムも任意の機能をシミュレートできるのに、なぜ人工ニューラルネットワークを発明するのでしょうか。