Neural Network

What is Neural Network?
1. Dive into the neuron
2. How does a neural network simulate an arbitrary function
3. Why do we need neural networks
How to construct a neural network
1. Fully connected neural network
2. Use graphical tool to design neural network
3. The "activation function" of the output layer
How to train a neural network
1. Learning algorithm and principle
2. Build and train neural networks from scratch
3. Rewrite the code using PyTorch
4. Use graphical tool to train neural network
Some important problems of neural network
1. Network structure
2. Overfitting
3. Underfitting
4. Overfitting vs underfitting
5. Initialization
6. Vanishing gradient and exploding gradient
Convolutional Neural Network(CNN)
1. 1D-convolution
2. 1D-convolution experiments
3. 1D-pooling
4. 1D-CNN experiments
5. 2D-CNN
6. 2D-CNN experiments
Recurrent Neural Network(RNN)
1. Vanilla RNN
2. Seq2seq, Autoencoder, Encoder-Decoder
3. Advanced RNN
4. RNN classification experiment
Natural language processing
1. Embedding: Convert symbols to values
2. Text Classification 1
3. Text Classification 2
4. TextCNN
5. Entity recognition
6. Word segmentation, POS tagging and chunking
7. Sequence tagging in action
8. Bidirectional RNN
9. BI-LSTM-CRF
10. Attention
Language Models
1. n-gram Model: Unigram
2. n-gram Model: Bigram
3. n-gram Model: Trigram
4. RNN Language Model
5. Transformer Language Model
Linear Algebra
1. Vector
2. Matrix
3. Dive in matrix multiplication
4. Tensor

What is Neural Network?

Overview

In short, a neural network can be viewed as a function: it takes input data and generates output results.

Defining Functions

We illustrate the function form of a neural network through MNIST Handwritten Digit Recognition:

Task Type: Image Classification
Input: Each 28 x 28 image, consisting of 784 pixels, each represented by a real number
Output: Digits 0-9
Task Description: Identify the unique digit from the image
Function Definition:

\begin{aligned} y &= f(x_1, x_2, ..., x_{784}) \\ &x_i \in \mathbb R, i = 1, ..., 784 \\ &y \in \{0, 1, ..., 9\} \end{aligned}

This is an entry-level application of a neural network. The input is a low-resolution (28 x 28) black-and-white image, with 784 input variables. If the input were a million-pixel color image, the corresponding input variables would reach over 3 million.

Hence, neural networks solve complex problems by constructing complex functions. Implementing algorithms means constructing these functions.

How to construct such complex functions? We can start with simple functions, such as digital circuits.

Digital Circuits

Digital circuits are the cornerstone of modern computing, but at their core, they consist of simple AND, OR, and NOT logic gates.

What are logic gates? Essentially, they are the simplest functions.

Logic Gate	Expression	Function Form
AND Gate	$x \land y$	$z = \land(x, y)$
OR Gate	$x \lor y$	$z = \lor(x, y)$
NOT Gate	$\lnot x$	$y = \lnot(x)$

Variable type: All boolean variables, only 2 values: $\{T, F\}$ , much simpler than natural numbers ( $\mathbb N$ ) and real numbers ( $\mathbb R$ ).
Number of variables: unary or binary function, which is also the simplest form of function
Function representation: use truth table for description. Why not use images? Because it is a discrete function, there are some isolated points on the image, which is not very attractive.

NOT gate

$x$	$\lnot x$
$T$	$F$
$F$	$T$

NOT gate image (use 0 for $F$ and 1 for $T$ )

AND gate, OR gate

$x$	$y$	$x \land y$	$x \lor y$
$T$	$T$	$T$	$T$
$T$	$F$	$F$	$T$
$F$	$T$	$F$	$T$
$F$	$F$	$F$	$F$

AND gate image

OR gate image

Combining Logic Gates

By combining simple logic gates, one can construct more complex functions.

for@example, to create new binary functions:

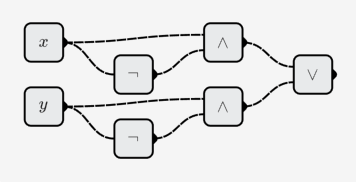
XOR: $x \oplus y = (x \land \lnot y) \lor (\lnot x \land y)$

XNOR: $x \odot y = (x \land y) \lor (\lnot x \land \lnot y)$

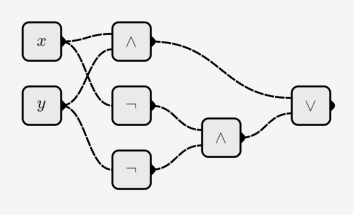
Construct a multivariate function:

3-bit AND operation: $f(x, y, z) = x \land y \land z$

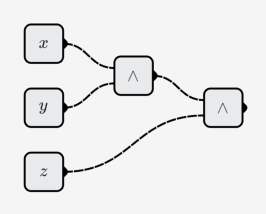
8-bit adder: $f(x_1, ..., x_8, y_1, ..., y_8)$ $f (x_{1}, ..., x_{8}, y_{1}, ..., y_{8})$
- It is a 16-element function containing 16 Boolean variables
32-bit adder: $f(x*1, ..., x*{32}, y*1, ..., y*{32})$ $f (x * 1, ..., x * 32, y * 1, ..., y * 32)$
- It is a 64-element function containing 64 Boolean variables
- It can also be regarded as a binary function of 32-bit integers: $f(x, y) \quad x, y \in \text{Int32}$

Summary

By combining simple logic gate functions, new logic functions can be constructed. Including operations such as addition, subtraction, multiplication, and division of 32-bit integers, and operations of 32-bit single-precision floating-point types, etc.

Programming language

Let's look at programming languages again. Take Python as an example, look at the elements in Python.

Operator

Name	Symbol	Function
Logical operators	and or not	Binary and unary logic functions
Arithmetic Operators	+, -, , /, %, *, //	Binary Functions
Comparison operators	==, !=, >, <, >=, <=	Binary functions
...

Taking the floating-point number addition operator (+) as an example, the function image is as follows:

$f(x, y) = x + y$

Functions

You can define your own functions in Python:

def f(x, y):
    return max(0, 2*x + 3*y - 3)

A new function is defined here. It uses "+, -, *, max" and other functions to construct the new function. The method of construction is also through the composition of functions.

Summary

Functions are everywhere in programming languages. By combining basic functions, new functions can be constructed and new algorithms can be obtained.

Neural Network

Neural network is also function. Like digital circuits and programming languages, it is also composed of simple functions. The basic units of digital circuits are logical functions such as AND, OR, and NOT. The basic units in programming languages are functions such as various operators, while the basic unit of neural networks is neurons.

Neuron

So what is a neuron? A biological neuron is a cell with input dendrites and output axons. And the neuron on the neural network is an artificial neuron, it is also a function, more precisely, it is a kind of function.

The number of inputs of neurons can be changed, which means that it represents a $n$ -element function $f(x_1, ..., x_n)$ , and $n$ can be different for different neurons.

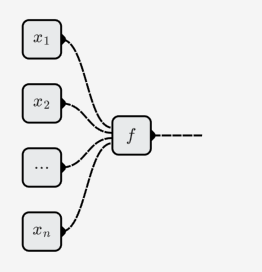
Neural Network

Neurons combine with each other to form a neural network. As shown below:

A neural network is a function composed of neuron functions. A neuron function is a function composed of simple functions, such as AND, OR, and NOT.

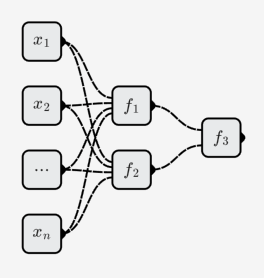
The neural network contains three neurons(do not count input neurons):

$f_1(x_1, ..., x_n)$
$f_2(x_1, ..., x_n)$
$f_3(x_1, x_2)$

The function represented by the neural network is:

f(x_1, ..., x_n) = f_3(f_1(x_1, ..., x_n), f_2(x_1, ..., x_n))

Summary

The core of the digital circuits (hardware) is function, and its basic functions are the AND OR NOT logic gate functions;
The core of programming languages (software) is function, and its basic functions are various operator functions and built-in functions (provided by hardware or compounded);
The core of neural networks is also function, and its basic functions are neurons;
New functions can be constructed through the composition of simple functions. Neural networks are functions constructed from neuron functions through function composition operations.

Question

What exactly is the function represented by a neuron?

Just knowing that it is a $n$ -element function is not enough. The basic units AND, OR, and NOT gates in digital circuits all list the truth table and draw the figure, but what about the neuron?