Neural Network

한국어

신경망이란
1. 뉴런에 뛰어들다
2. 신경망은 어떻게 임의의 기능을 시뮬레이션합니까?
3. 신경망이 필요한 이유
신경망을 구성하는 방법
1. 완전히 연결된 신경망
2. 그래픽 도구를 사용하여 신경망 설계
3. 출력 레이어의 "활성화 기능"
신경망을 훈련시키는 방법
1. 학습 알고리즘 및 원리
2. 처음부터 신경망 구축 및 훈련
3. PyTorch를 사용하여 코드 다시 작성
4. 그래픽 도구를 사용하여 신경망 훈련
신경망의 몇 가지 중요한 문제
1. 네트워크 구조
2. 과적합
3. 언더피팅
4. 과적합 대 과소적합
5. 초기화
6. 그라디언트 소멸 및 그라디언트 폭발
합성곱 신경망(CNN)
1. 1D 컨볼루션
2. 1D 컨볼루션 실험
3. 1D 풀링
4. 1D-CNN 실험
5. 2D-CNN
6. 2D-CNN 실험
순환 신경망(RNN)
1. 바닐라 RNN
2. Seq2seq, Autoencoder, Encoder-Decoder
3. 고급 RNN
4. RNN 분류 실험
자연어 처리
1. Embedding: 기호를 값으로 변환
2. 텍스트 분류 1
3. 텍스트 분류 2
4. TextCNN
5. 엔티티 인식
6. 단어 분할, 품사 태깅 및 청크
7. 작동 중인 시퀀스 태깅
8. 양방향 RNN
9. BI-LSTM-CRF
10. 주목
언어 모델
1. n-gram 모델: 언어 모델
2. n-gram 모델: 바이그램 모델
3. n-gram 모델: 트라이그램 모델
4. RNN 언어 모델
5. Transformer 언어 모델
선형 대수학
1. 벡터
2. 매트릭스
3. 행렬 곱셈에 대해 자세히 알아보기
4. 텐서

뉴런에 뛰어들다

개요

이전 섹션(신경망이란?)에서 신경망은 뉴런으로 구성된 함수이며 뉴런도 함수라는 것을 배웠습니다.

뉴런은 계속해서 2개의 하위 기능으로 나눌 수 있습니다.

$n$ 요소 선형 함수: $g(x_1, ..., x_n)$
단항 비선형 함수: $h(x)$

뉴런이 나타내는 기능은 다음과 같습니다.

f(x_1, ..., x_n) = h(g(x_1, ..., x_n))

선형 함수 $g(x_1, ..., x_n)$

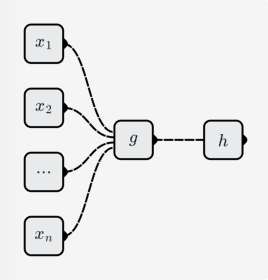
선형 함수의 형식은 다음과 같습니다.

g(x_1, ..., x_n) = w_1x_1 + ..., w_nx_n + b

그 중 $w_1, ..., w_n, b$ 는 모두 매개변수이며 선형 함수마다 매개변수가 다릅니다.

단항 선형 함수

$n = 1$ , $g(x_1) = w_1x_1 + b$ 일 때 함수 이미지는 직선입니다.


 $w_1$ 1
 $b$ 0

이진 선형 함수

$n = 2$ , $g(x_1, x_2) = w_1x_1 + w_2x_2 + b$ 일 때 함수 이미지는 평면입니다.


 $w_1$ 0
 $w_2$ 1
 $b$ 0

$n$ 요소 선형 함수

$n > 2$ 일 때 함수 이미지는 초평면입니다. 3D를 넘어서는 시각화는 편리하지 않습니다. 그러나 그 특성이 직선적이라고 상상할 수 있습니다.

비선형 함수 $h(x)$

비선형 함수는 선형 함수와 다른 함수라는 이름에서 이해하기 쉽습니다. 선형 함수는 직선이고 비선형 함수는 곡선입니다. 가장 일반적인 sigmoid 함수와 같은:

활성화 기능

신경망에서는 이 단항 비선형 함수를 활성화 함수라고 부릅니다. 몇 가지 일반적인 활성화 기능에 대해서는 지식 기반의 활성화 기능을 참조하십시오. 여기서:

Linear: $f(x) = x$ 는 선형 함수이므로 비선형 함수를 사용하지 않습니다.
Softmax 는 특수한 경우입니다. 엄밀히 말하면 활성화 함수가 아닙니다.

필요성

비선형 활성화 함수 다음에 선형 함수가 와야 하는 이유는 무엇입니까?

이 때문입니다:

뉴런이 모두 선형 함수라면 뉴런으로 구성된 신경망도 선형 함수입니다.

예를 들면 다음과 같습니다.

$f_1(x, y) = w_1x + w_2y + b_1$
$f_2(x, y) = w_3x + w_4y + b_2$
$f_3(x, y) = w_5x + w_6y + b_3$

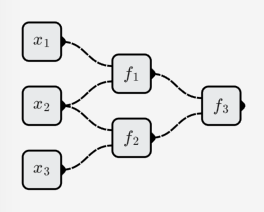
그러면 전체 신경망이 나타내는 함수는 다음과 같습니다.

\begin{aligned} &f_3(f_1(x_1, x_2, x_3), f_2(x_1, x_2, x_3)) \\ = &w_5(w_1x_1 + w_2x_2 + b_1) + w_6(w_3x_2 + w_4x_3 + b_2) + b_3 \\ = &(w_1w_5)x_1 + (w_2w_5 + w_3w_6)x_2 + (w_4w_6)x_3 + (w_5b_1 + w_6b_2 + b_3) \\ \end{aligned}

이것은 삼항 선형 함수입니다.

우리가 구성해야 하는 목적 함수는 다양한 함수를 포함하며 선형 함수는 그 중 하나일 뿐입니다.

우리는 신경망이 선형 함수뿐만 아니라 임의의 함수를 시뮬레이션할 수 있기를 바랍니다. 그래서 우리는 비선형 활성화 함수를 추가하고 선형 함수를 "구부렸습니다".

완전한 뉴런

완전한 뉴런은 선형 함수와 비선형 활성화 함수를 결합하여 더 흥미롭고 강력하게 만듭니다.

단항 함수

$n = 1$ , $g(x_1) = w_1x_1 + b$ 일 때 sigmoid 활성화 함수를 사용하여 뉴런의 해당 함수는 다음과 같습니다.

h(g(x))=\text{sigmoid}(wx + b)

기능 이미지는 다음과 같습니다.


 $w$ 1
 $b$ 0

이진 함수

$n = 2$ , $g(x_1, x_2) = w_1x_1 + w_2x_2 + b$ 일 때 sigmoid 활성화 함수를 사용하여 뉴런의 해당 함수는 다음과 같습니다.

h(g(x))=\text{sigmoid}(w_1x_1 + w_2x_2 + b)

기능 이미지는 다음과 같습니다.


 $w_1$ 0
 $w_2$ 1
 $b$ 0

$n$ -요소 함수

시각화 문제로 인해 여기에서는 전적으로 내 상상에 달려 있습니다! 😥

질문

신경망이 뉴런 조합에서 복잡한 기능을 시뮬레이션할 수 있는 이유는 무엇입니까?

간단한 뉴런을 통해 조금 더 복잡한 기능을 시뮬레이션하는 방법을 직관적으로 상상할 수 있습니다.