Neural Network

Français

Qu'est-ce que le réseau de neurones
1. Plongez dans le neurone
2. Comment un réseau de neurones simule-t-il une fonction arbitraire
3. Pourquoi avons-nous besoin de réseaux de neurones
Comment construire un réseau de neurones
1. Réseau de neurones entièrement connecté
2. Utiliser un outil graphique pour concevoir un réseau de neurones
3. La "fonction d'activation" de la couche de sortie
Comment entraîner un réseau de neurones
1. Algorithme et principe d'apprentissage
2. Construisez et entraînez des réseaux de neurones à partir de zéro
3. Réécrire le code à l'aide de PyTorch
4. Utiliser un outil graphique pour entraîner le réseau de neurones
Quelques problèmes importants de réseau de neurones
1. Structure du réseau
2. Surapprentissage
3. Insuffisance
4. Surapprentissage vs sous-apprentissage
5. Initialisation
6. Dégradé disparaissant et dégradé explosif
Réseau de neurones convolutifs (CNN)
1. 1D-convolution
2. Expériences de convolution 1D
3. Mise en commun 1D
4. Expériences 1D-CNN
5. 2D-CNN
6. Expériences 2D-CNN
Réseau de neurones récurrents (RNN)
1. Vanille RNN
2. Seq2seq, Autoencoder, Encoder-Decoder
3. RNN avancé
4. Expérience de classification RNN
Traitement du langage naturel
1. Embedding: convertir des symboles en valeurs
2. Classification de texte 1
3. Classification de texte 2
4. TextCNN
5. Reconnaissance d'entité
6. Segmentation de mots, étiquetage et découpage de parties de discours
7. Marquage de séquence en action
8. RNN bidirectionnel
9. BI-LSTM-CRF
10. Attention
Modèles de langage
1. Modèle unigramme
2. Modèle bigramme
3. Modèle trigramme
4. Modèle RNN de langage
5. Modèle Transformer de langage
Algèbre linéaire
1. Vecteur
2. Matrice
3. Plonger dans la multiplication matricielle
4. Tenseur

Qu'est-ce que le réseau de neurones

Aperçu

En bref, le réseau de neurones est une fonction: données d'entrée, résultat de sortie.

Fonction

Prenons l'exemple de la reconnaissance d'images de chiffres manuscrits MNIST pour définir la forme de fonction correspondante:

Type de tâche: Classification des images
Entrée: Une image contient 28 x 28=784 pixels, et chaque pixel est représenté par un nombre réel
Sortie: 0-9
Description de la tâche: Identifiez le numéro unique à partir de l'image
Définition de la fonction

\begin{aligned} y &= f(x_1, x_2, ..., x_{784}) \\ &x_i \in \mathbb R, i = 1, ..., 784 \\ &y \in \{0, 1, ..., 9\} \end{aligned}

Il s'agit d'une application d'entrée de gamme de Neural Network. L'entrée est une image en niveaux de gris basse résolution (28 x 28), correspondant à une fonction avec 784 variables d'entrée. S'il s'agit d'une image couleur mégapixel, les variables d'entrée correspondantes atteindront 3 millions.

On peut voir que le réseau de neurones est utilisé pour résoudre certains problèmes complexes, et les fonctions correspondantes sont également complexes. La réalisation de l'algorithme consiste à construire la fonction correspondante.

Comment construire une fonction aussi compliquée ? Nous pouvons commencer avec des fonctions simples. L'exemple le plus simple et le plus réussi est celui des circuits numériques.

Circuits numériques

Les circuits numériques sont les pierres angulaires des ordinateurs et ont construit notre immense monde numérique. Mais son noyau est composé de portes logiques AND, OR et NOT.

Qu'est-ce qu'une porte logique ? C'est en fait une fonction. Et ce sont les fonctions les plus simples.

Porte logique	expression	forme de fonction
AND portail	$x \land y$	$z = \land(x, y)$
OR portail	$x \lor y$	$z = \lor(x, y)$
NOT portail	$\lnot x$	$y = \lnot(x)$

Type de variable: Toutes les variables booléennes, seulement 2 valeurs: $\{T, F\}$ , beaucoup plus simple que les nombres naturels ( $\mathbb N$ ) et les nombres réels ( $\mathbb R$ ).
Nombre de variables: fonction unaire ou binaire, qui est aussi la forme de fonction la plus simple
Représentation de fonction: utiliser la table de vérité pour la description. Pourquoi ne pas utiliser des images ? Comme il s'agit d'une fonction discrète, il y a des points isolés sur l'image, ce qui n'est pas très attractif.

NOT porte

$x$	$\lnot x$
$T$	$F$
$F$	$T$

NOT porte image (utilisez 0 pour $F$ et 1 pour $T$ )

AND porte、OR porte

$x$	$y$	$x \land y$	$x \lor y$
$T$	$T$	$T$	$T$
$T$	$F$	$F$	$T$
$F$	$T$	$F$	$T$
$F$	$F$	$F$	$F$

AND image de porte

OR image de porte

Porte logique de combinaison

Combinez des portes logiques simples pour obtenir des fonctions plus puissantes.

Construisez une nouvelle fonction binaire:

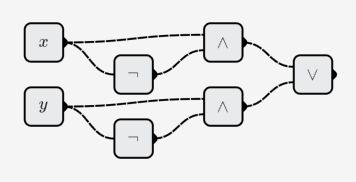
XOR: $x \oplus y = (x \land \lnot y) \lor (\lnot x \land y)$

XNOR: $x \odot y = (x \land y) \lor (\lnot x \land \lnot y)$

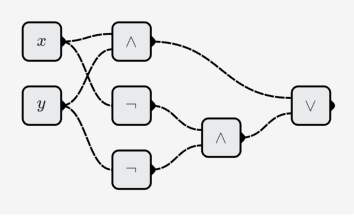
Construire une fonction multivariée:

Opération AND 3 bits: $f(x, y, z) = x \land y \land z$

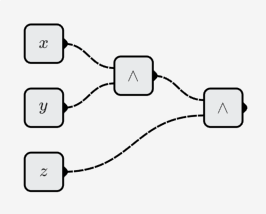
Additionneur 8 bits: $f(x_1, ..., x_8, y_1, ..., y_8)$ $f (x_{1}, ..., x_{8}, y_{1}, ..., y_{8})$
- C'est une fonction à 16 éléments contenant 16 variables booléennes
Additionneur 32 bits: $f(x*1, ..., x*{32}, y*1, ..., y*{32})$ $f (x * 1, ..., x * 32, y * 1, ..., y * 32)$
- C'est une fonction à 64 éléments contenant 64 variables booléennes
- Elle peut aussi être considérée comme une fonction binaire d'entiers 32 bits: $f(x, y) \quad x, y \in \text{Int32}$

Résumer

En combinant des fonctions de portes logiques simples, de nouvelles fonctions logiques peuvent être construites. Y compris les opérations telles que l'addition, la soustraction, la multiplication et la division d'entiers 32 bits, et les opérations de types à virgule flottante simple précision 32 bits, etc.

Langage de programmation

Regardons à nouveau les langages de programmation. Prenez Python comme exemple, regardez les éléments en Python.

Opérateur

Nom	Symbole	Fonction
Opérateurs logiques	and or not	Fonctions logiques binaires et unaires
Opérateurs arithmétiques	+, -, , /, %, *, //	Fonctions binaires
Opérateurs de comparaison	==, !=, >, <, >=, <=	Fonctions binaires
...

En prenant l'opérateur d'addition de nombre à virgule flottante (+) comme exemple, l'image de la fonction est la suivante:

$f(x, y) = x + y$

Les fonctions

Vous pouvez définir vos propres fonctions en Python:

def f(x, y):
    return max(0, 2*x + 3*y - 3)

Une nouvelle fonction est définie ici. Il utilise "+, -, *, max" et d'autres fonctions pour construire la nouvelle fonction. Le mode de construction passe aussi par la composition de fonctions.

Résumer

Les fonctions sont partout dans les langages de programmation. En combinant des fonctions de base, de nouvelles fonctions peuvent être construites et de nouveaux algorithmes peuvent être obtenus.

Réseau neuronal

Le réseau de neurones est également fonction. Comme les circuits numériques et les langages de programmation, il est également composé de fonctions simples. Les unités de base des circuits numériques sont des fonctions logiques telles que AND, OR et NOT. Les unités de base des langages de programmation sont des fonctions telles que divers opérateurs, tandis que l'unité de base des réseaux de neurones sont les neurones.

Neurone

Alors, qu'est-ce qu'un neurone ? Un neurone biologique est une cellule avec des dendrites d'entrée et des axones de sortie. Et le neurone sur le réseau de neurones est un neurone artificiel, c'est aussi une fonction, plus précisément, c'est une sorte de fonction.

Le nombre d'entrées de neurones peut être modifié, ce qui signifie qu'il représente une fonction d'élément $n$ $f(x_1, ..., x_n)$ , et $n$ peut être différent pour différents neurones.

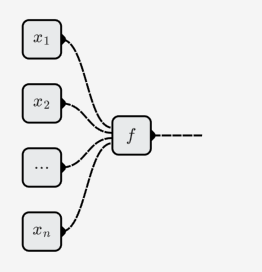
Réseau neuronal

Les neurones se combinent pour former un réseau de neurones. Comme indiqué ci-dessous:

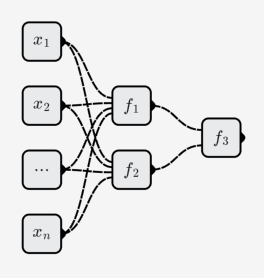
Le réseau de neurones contient trois neurones (ne comptez pas les neurones d'entrée):

$f_1(x_1, ..., x_n)$
$f_2(x_1, ..., x_n)$
$f_3(x_1, x_2)$

La fonction représentée par le réseau de neurones est:

f(x_1, ..., x_n) = f_3(f_1(x_1, ..., x_n), f_2(x_1, ..., x_n))

Résumer

Le cœur des circuits numériques (matériel) est la fonction, et ses fonctions de base sont les fonctions de porte logique AND OR NOT;
Le noyau des langages de programmation (logiciels) est la fonction, et ses fonctions de base sont diverses fonctions d'opérateur et fonctions intégrées (fournies par le matériel ou composées);
Le cœur des réseaux de neurones est aussi la fonction, et ses fonctions de base sont les neurones ;
De nouvelles fonctions peuvent être construites par la composition de fonctions simples. Les réseaux de neurones sont des fonctions construites à partir de fonctions neuronales par le biais d'opérations de composition de fonctions.

Question

Quelle est exactement la fonction représentée par un neurone ?

Il ne suffit pas de savoir qu'il s'agit d'une fonction d'élément $n$ . Les unités de base AND, OR et NOT des portes dans les circuits numériques énumèrent toutes la table de vérité et dessinent la figure, mais qu'en est-il du neurone ?