Neural Network

Español

¿Qué es la red neuronal?
1. Sumérgete en la neurona
2. ¿Cómo simula una red neuronal una función arbitraria?
3. ¿Por qué necesitamos redes neuronales?
Cómo construir una red neuronal
1. Red neuronal completamente conectada
2. Utilice una herramienta gráfica para diseñar una red neuronal
3. La "función de activación" de la capa de salida
Cómo entrenar una red neuronal
1. Principio y algoritmo de aprendizaje
2. Construya y entrene redes neuronales desde cero
3. Reescribe el código usando PyTorch
4. Utilice una herramienta gráfica para entrenar la red neuronal
Algunos problemas importantes de la red neuronal
1. Estructura de red
2. Sobreajuste
3. Desajuste
4. Sobreajuste vs desajuste
5. Inicialización
6. Gradiente de desaparición y gradiente explosivo
Red neuronal convolucional (CNN)
1. Convolución 1D
2. Experimentos de convolución 1D
3. agrupación 1D
4. Experimentos 1D-CNN
5. 2D-CNN
6. Experimentos 2D-CNN
Red neuronal recurrente (RNN)
1. Vanilla RNN
2. Seq2seq, Autoencoder, Encoder-Decoder
3. RNN avanzado
4. Experimento de clasificación RNN
Procesamiento natural del lenguaje
1. Embedding: convierte símbolos en valores
2. Clasificación de texto 1
3. Clasificación de texto 2
4. TextCNN
5. Reconocimiento de entidad
6. Segmentación de palabras, etiquetado y fragmentación de parte del discurso
7. Etiquetado de secuencia en acción
8. RNN bidireccional
9. BI-LSTM-CRF
10. Atención
Modelos de lenguaje
1. Modelo n-grama: Unigrama
2. Modelo n-grama: Bigrama
3. Modelo n-grama: Trigrama
4. Modelo de lenguaje RNN
5. Modelo de lenguaje Transformer
Álgebra lineal
1. Vector
2. Matriz
3. Sumérgete en la multiplicación de matrices
4. Tensor

¿Qué es la red neuronal?

Visión general

En resumen, la red neuronal es una función: datos de entrada, resultado de salida.

Función

Tomemos reconocimiento de imágenes de dígitos manuscritos de MNIST como ejemplo para definir la forma de función correspondiente:

Tipo de tarea: clasificación de imágenes
Entrada: una imagen contiene 28 x 28 = 784 píxeles, y cada píxel está representado por un número real
Salida: 0-9
Descripción de la tarea: identifica el número único de la imagen
Definición de función

\begin{aligned} y &= f(x_1, x_2, ..., x_{784}) \\ &x_i \in \mathbb R, i = 1, ..., 784 \\ &y \in \{0, 1, ..., 9\} \end{aligned}

Esta es una aplicación de nivel de entrada de Neural Network. La entrada es una imagen en escala de grises de baja resolución (28 x 28), correspondiente a una función con 784 variables de entrada. Si se trata de una imagen en color de megapíxeles, las variables de entrada correspondientes alcanzarán los 3 millones.

Se puede ver que la red neuronal se usa para resolver algunos problemas complejos, y las funciones correspondientes también son complejas. La realización del algoritmo consiste en construir la función correspondiente.

¿Cómo construir una función tan complicada? Podemos comenzar con funciones simples. El ejemplo más simple y exitoso son los circuitos digitales.

Circuitos digitales

Los circuitos digitales son la piedra angular de las computadoras y han construido nuestro enorme mundo digital. Pero su núcleo se compone de puertas lógicas AND, OR y NOT.

¿Qué es una puerta lógica? De hecho, es una función. Y son las funciones más simples.

Puerta lógica	expresión	forma de función
AND puerta	$x \land y$	$z = \land(x, y)$
Puerta OR	$x \lor y$	$z = \lor(x, y)$
NOT puerta	$\lnot x$	$y = \lnot(x)$

Tipo de variable: Todas las variables booleanas, solo 2 valores: $\{T, F\}$ , mucho más simple que los números naturales ( $\mathbb N$ ) y los números reales ( $\mathbb R$ ).
Número de variables: función unaria o binaria, que también es la forma más simple de función
Representación de funciones: use la tabla de verdad para la descripción. ¿Por qué no utilizar imágenes? Por ser una función discreta, hay algunos puntos aislados en la imagen, lo que no resulta muy atractivo.

NOT puerta

$x$	$\lnot x$
$T$	$F$
$F$	$T$

NOT imagen de puerta (use 0 para $F$ y 1 para $T$ )

AND puerta 、 OR puerta

$x$	$y$	$x \land y$	$x \lor y$
$T$	$T$	$T$	$T$
$T$	$F$	$F$	$T$
$F$	$T$	$F$	$T$
$F$	$F$	$F$	$F$

AND imagen de puerta

OR imagen de puerta

Puerta lógica combinada

Combine puertas lógicas simples para obtener funciones más potentes.

Construya una nueva función binaria:

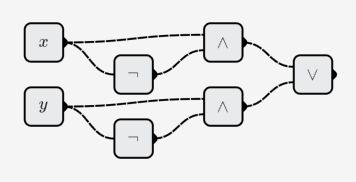
XOR: $x \oplus y = (x \land \lnot y) \lor (\lnot x \land y)$

XNOR: $x \odot y = (x \land y) \lor (\lnot x \land \lnot y)$

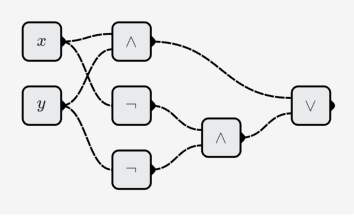
Construya una función multivariante:

Operación AND de 3 bits: $f(x, y, z) = x \land y \land z$

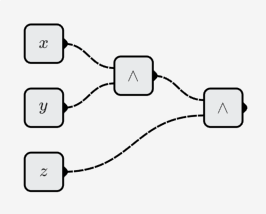
Sumador de 8 bits: $f(x_1, ..., x_8, y_1, ..., y_8)$ $f (x_{1}, ..., x_{8}, y_{1}, ..., y_{8})$
- Es una función de 16 elementos que contiene 16 variables booleanas
Sumador de 32 bits: $f(x*1, ..., x*{32}, y*1, ..., y*{32})$ $f (x * 1, ..., x * 32, y * 1, ..., y * 32)$
- Es una función de 64 elementos que contiene 64 variables booleanas
- También se puede considerar como una función binaria de enteros de 32 bits: $f(x, y) \quad x, y \in \text{Int32}$

Resumir

Combinando funciones de compuerta lógica simples, se pueden construir nuevas funciones lógicas. Incluyendo operaciones como suma, resta, multiplicación y división de enteros de 32 bits y operaciones de tipos de coma flotante de precisión simple de 32 bits, etc.

Lenguaje de programación

Veamos nuevamente los lenguajes de programación. Tome Python como ejemplo, observe los elementos en Python.

Operador

Nombre	Símbolo	Función
Operadores lógicos	and or not	Funciones lógicas binarias y unarias
Operadores aritméticos	+, -, , /,%, *, //	Funciones binarias
Operadores de comparación	==,! =,>, <,>=, <=	Funciones binarias
...

Tomando el operador de suma de números de punto flotante (+) como ejemplo, la imagen de la función es la siguiente:

$f(x, y) = x + y$

Funciones

Puede definir sus propias funciones en Python:

def f(x, y):
    return max(0, 2*x + 3*y - 3)

Aquí se define una nueva función. Utiliza "+, -, *, max" y otras funciones para construir la nueva función. El método de construcción también es a través de la composición de funciones.

Resumir

Las funciones están en todas partes en los lenguajes de programación. Combinando funciones básicas, se pueden construir nuevas funciones y se pueden obtener nuevos algoritmos.

Red neuronal

La red neuronal también funciona. Al igual que los circuitos digitales y los lenguajes de programación, también se compone de funciones simples. Las unidades básicas de los circuitos digitales son funciones lógicas como Y, O y NO. Las unidades básicas en los lenguajes de programación son funciones como varios operadores, mientras que la unidad básica de las redes neuronales son las neuronas.

Neurona

Entonces, ¿qué es una neurona? Una neurona biológica es una célula con dendritas de entrada y axones de salida. Y la neurona de la red neuronal es una neurona artificial, también es una función, más precisamente, es una especie de función.

El número de entradas de neuronas se puede cambiar, lo que significa que representa una función de elemento $n$ $f(x_1, ..., x_n)$ , y $n$ puede ser diferente para diferentes neuronas.

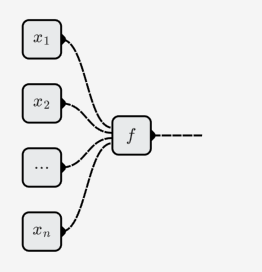
Red neuronal

Las neuronas se combinan entre sí para formar una red neuronal. Como se muestra abajo:

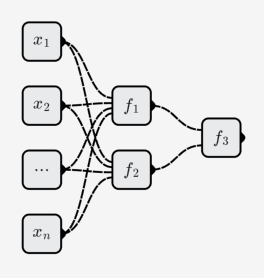
La red neuronal contiene tres neuronas (no cuente las neuronas de entrada):

$f_1(x_1, ..., x_n)$
$f_2(x_1, ..., x_n)$
$f_3(x_1, x_2)$

La función representada por la red neuronal es:

f(x_1, ..., x_n) = f_3(f_1(x_1, ..., x_n), f_2(x_1, ..., x_n))

Resumir

El núcleo de los circuitos digitales (hardware) es la función, y sus funciones básicas son las funciones de puerta lógica Y O NO;
El núcleo de los lenguajes de programación (software) es la función, y sus funciones básicas son varias funciones de operador y funciones integradas (proporcionadas por hardware o compuestas);
El núcleo de las redes neuronales también es la función, y sus funciones básicas son las neuronas;
Se pueden construir nuevas funciones mediante la composición de funciones simples. Las redes neuronales son funciones construidas a partir de funciones neuronales mediante operaciones de composición de funciones.

Pregunta

¿Cuál es exactamente la función representada por una neurona?

El simple hecho de saber que es una función de elemento $n$ no es suficiente. Las unidades básicas Y, O y NO puertas en circuitos digitales enumeran la tabla de verdad y dibujan la figura, pero ¿qué pasa con la neurona?