Neural Network

Deutsch

Was ist ein neuronales Netzwerk?
1. Tauchen Sie ein in das Neuron
2. Wie simuliert ein neuronales Netz eine beliebige Funktion
3. Warum brauchen wir neuronale Netze
Wie baut man ein neuronales Netz auf?
1. Vollständig verbundenes neuronales Netzwerk
2. Verwenden Sie ein grafisches Tool, um ein neuronales Netzwerk zu entwerfen
3. Die "Aktivierungsfunktion" der Ausgabeschicht
So trainieren Sie ein neuronales Netz
1. Lernalgorithmus und -prinzip
2. Erstellen und trainieren Sie neuronale Netze von Grund auf neu
3. Schreiben Sie den Code mit PyTorch um
4. Verwenden Sie ein grafisches Tool, um das neuronale Netzwerk zu trainieren
Einige wichtige Probleme des neuronalen Netzes
1. Netzwerkstruktur
2. Überanpassung
3. Unteranpassung
4. Überanpassung vs. Unteranpassung
5. Initialisierung
6. Verschwindender Gradient und explodierender Gradient
Convolutional Neural Network (CNN)
1. 1D-Faltung
2. 1D-Faltungsexperimente
3. 1D-Pooling
4. 1D-CNN-Experimente
5. 2D-CNN
6. 2D-CNN Experimente
Rekurrentes neuronales Netz (RNN)
1. Vanille RNN
2. Seq2seq, Autoencoder, Encoder-Decoder
3. Erweiterte RNN
4. RNN-Klassifikationsexperiment
Verarbeitung natürlicher Sprache
1. Embedding: Symbole in Werte umwandeln
2. Textkategorisierung 1
3. Textkategorisierung 2
4. TextCNN
5. Entitätserkennung
6. Wortsegmentierung, Wortart-Tagging und Chunking
7. Sequenz-Tagging in Aktion
8. Bidirektionales RNN
9. BI-LSTM-CRF
10. Beachtung
Sprachmodelle
1. n-gram-Modelle: Unigram
2. n-gram-Modelle: Bigram
3. n-gram-Modelle: Trigram
4. RNN-Sprachmodelle
5. Transformer-Sprachmodelle
Lineare Algebra
1. Vektor
2. Matrix
3. Eintauchen in die Matrixmultiplikation
4. Tensor

Was ist ein neuronales Netzwerk?

Überblick

Kurz gesagt, Neuronales Netzwerk ist eine Funktion: Eingabedaten, Ausgabeergebnis.

Funktion

Nehmen wir als Beispiel MNIST handschriftliche Ziffernbilderkennung, um die entsprechende Funktionsform zu definieren:

Aufgabentyp: Bildklassifizierung
Eingabe: Ein Bild enthält 28 x 28 = 784 Pixel, und jedes Pixel wird durch eine reelle Zahl dargestellt
Ausgabe: 0-9
Aufgabenbeschreibung: Identifizieren Sie die eindeutige Nummer aus dem Bild
Funktionsdefinition

\begin{aligned} y &= f(x_1, x_2, ..., x_{784}) \\ &x_i \in \mathbb R, i = 1, ..., 784 \\ &y \in \{0, 1, ..., 9\} \end{aligned}

Dies ist eine Einstiegsanwendung des neuronalen Netzes. Die Eingabe ist ein Graustufenbild mit niedriger Auflösung (28 x 28), das einer Funktion mit 784 Eingabevariablen entspricht. Wenn es sich um ein Megapixel-Farbbild handelt, erreichen die entsprechenden Eingabevariablen 3 Millionen.

Es ist ersichtlich, dass das neuronale Netz zur Lösung einiger komplexer Probleme verwendet wird und die entsprechenden Funktionen ebenfalls komplex sind. Die Realisierung des Algorithmus besteht darin, die entsprechende Funktion zu konstruieren.

Wie konstruiere ich eine so komplizierte Funktion? Wir können mit einfachen Funktionen beginnen. Das einfachste und erfolgreichste Beispiel sind digitale Schaltungen.

Digitale Schaltungen

Digitale Schaltkreise sind die Eckpfeiler von Computern und haben unsere riesige digitale Welt aufgebaut. Aber sein Kern besteht aus UND-, ODER- und NICHT-Logikgattern.

Was ist ein Logikgatter? Es ist eigentlich eine Funktion. Und das sind die einfachsten Funktionen.

Logikgatter	Ausdruck	Funktionsform
AND-Gatter	$x \land y$	$z = \land(x, y)$
OR-Tor	$x \lor y$	$z = \lor(x, y)$
NOT Tor	$\lnot x$	$y = \lnot(x)$

Variablentyp: Alle booleschen Variablen, nur 2 Werte: $\{T, F\}$ , viel einfacher als natürliche Zahlen ( $\mathbb N$ ) und reelle Zahlen ( $\mathbb R$ ).
Anzahl der Variablen: unäre oder binäre Funktion, die auch die einfachste Form der Funktion ist
Funktionsdarstellung: Wahrheitstabelle zur Beschreibung verwenden. Warum keine Bilder verwenden? Da es sich um eine diskrete Funktion handelt, gibt es einige isolierte Punkte auf dem Bild, die nicht sehr attraktiv sind.

NOT Tor

$x$	$\lnot x$
$T$	$F$
$F$	$T$

NOT Gate-Image (verwenden Sie 0 für $F$ und 1 für $T$ )

AND-Gatter、OR-Gatter

$x$	$y$	$x \land y$	$x \lor y$
$T$	$T$	$T$	$T$
$T$	$F$	$F$	$T$
$F$	$T$	$F$	$T$
$F$	$F$	$F$	$F$

AND-Gatter-Bild

OR-Gatter-Bild

Verknüpfungslogikgatter

Kombinieren Sie einfache Logikgatter, um leistungsfähigere Funktionen zu erhalten.

Konstruieren Sie eine neue Binärfunktion:

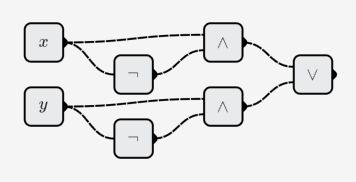
XOR: $x \oplus y = (x \land \lnot y) \lor (\lnot x \land y)$

XNOR: $x \odot y = (x \land y) \lor (\lnot x \land \lnot y)$

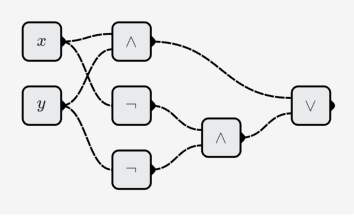
Konstruieren Sie eine multivariate Funktion:

3-Bit UND-Verknüpfung: $f(x, y, z) = x \land y \land z$

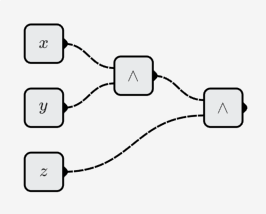
8-Bit-Addierer: $f(x_1, ..., x_8, y_1, ..., y_8)$ $f (x_{1}, ..., x_{8}, y_{1}, ..., y_{8})$
- Es handelt sich um eine 16-Elemente-Funktion mit 16 booleschen Variablen
32-Bit-Addierer: $f(x*1, ..., x*{32}, y*1, ..., y*{32})$ $f (x * 1, ..., x * 32, y * 1, ..., y * 32)$
- Es ist eine 64-Elemente-Funktion mit 64 booleschen Variablen
- Es kann auch als binäre Funktion von 32-Bit-Ganzzahlen betrachtet werden: $f(x, y) \quad x, y \in \text{Int32}$

Zusammenfassen

Durch Kombinieren einfacher Logikgatterfunktionen können neue Logikfunktionen konstruiert werden. Einschließlich Operationen wie Addition, Subtraktion, Multiplikation und Division von 32-Bit-Ganzzahlen und Operationen von 32-Bit-Gleitkommatypen mit einfacher Genauigkeit usw.

Programmiersprache

Schauen wir uns noch einmal die Programmiersprachen an. Nehmen Sie Python als Beispiel, schauen Sie sich die Elemente in Python an.

Operator

Name	Symbol	Funktion
Logische Operatoren	and or not	Binäre und unäre Logikfunktionen
Arithmetische Operatoren	+, -, , /, %, *, //	Binäre Funktionen
Vergleichsoperatoren	==, !=, >, <, >=, <=	Binäre Funktionen
...

Am Beispiel des Gleitkomma-Additionsoperators (+) sieht das Funktionsbild wie folgt aus:

$f(x, y) = x + y$

Funktionen

Sie können Ihre eigenen Funktionen in Python definieren:

def f(x, y):
    return max(0, 2*x + 3*y - 3)

Hier wird eine neue Funktion definiert. Es verwendet "+, -, *, max" und andere Funktionen, um die neue Funktion zu konstruieren. Die Konstruktionsmethode ist auch durch die Zusammensetzung von Funktionen.

Zusammenfassen

Funktionen sind überall in Programmiersprachen. Durch Kombinieren von Grundfunktionen können neue Funktionen konstruiert und neue Algorithmen erhalten werden.

Neurales Netzwerk

Neuronales Netz ist auch Funktion. Wie digitale Schaltungen und Programmiersprachen besteht auch sie aus einfachen Funktionen. Die Grundeinheiten digitaler Schaltungen sind logische Funktionen wie UND, ODER und NICHT. Die Grundeinheiten in Programmiersprachen sind Funktionen wie verschiedene Operatoren, während die Grundeinheit neuronaler Netze Neuronen sind.

Neuron

Was ist also ein Neuron? Ein biologisches Neuron ist eine Zelle mit Eingangsdendriten und Ausgangsaxonen. Und das Neuron im neuronalen Netz ist ein künstliches Neuron, es ist auch eine Funktion, genauer gesagt eine Art Funktion.

Die Anzahl der Eingänge von Neuronen kann verändert werden, d.h. es handelt sich um eine $n$ -Elementfunktion $f(x_1, ..., x_n)$ , und $n$ kann unterschiedlich sein Neuronen.

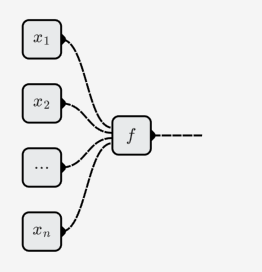
Neurales Netzwerk

Neuronen verbinden sich zu einem neuronalen Netz. Wie nachfolgend dargestellt:

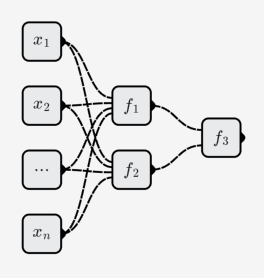
Das neuronale Netzwerk enthält drei Neuronen (zählen Sie keine Eingabeneuronen):

$f_1(x_1, ..., x_n)$
$f_2(x_1, ..., x_n)$
$f_3(x_1, x_2)$

Die durch das neuronale Netz repräsentierte Funktion ist:

f(x_1, ..., x_n) = f_3(f_1(x_1, ..., x_n), f_2(x_1, ..., x_n))

Zusammenfassen

Der Kern der digitalen Schaltungen (Hardware) ist die Funktion, und ihre Grundfunktionen sind die UND ODER NICHT-Logikgatterfunktionen;
Der Kern von Programmiersprachen (Software) ist die Funktion, und ihre Grundfunktionen sind verschiedene Operatorfunktionen und eingebaute Funktionen (bereitgestellt durch Hardware oder zusammengesetzt);
Der Kern neuronaler Netze ist auch die Funktion, und ihre Grundfunktionen sind Neuronen;
Neue Funktionen können durch die Komposition einfacher Funktionen konstruiert werden. Neuronale Netze sind Funktionen, die aus Neuronenfunktionen durch Funktionskompositionsoperationen konstruiert werden.

Frage

Was genau ist die Funktion eines Neurons?

Es reicht nicht aus, nur zu wissen, dass es sich um eine $n$ -Elementfunktion handelt. Die Grundeinheiten UND-, ODER- und NICHT-Gatter in digitalen Schaltungen listen alle die Wahrheitstabelle auf und zeichnen die Figur, aber was ist mit dem Neuron?