Neural Network

Italiano

Cos'è la rete neurale?
1. Immergiti nel neurone
2. In che modo una rete neurale simula una funzione arbitraria?
3. Perché abbiamo bisogno delle reti neurali?
Come costruire una rete neurale
1. Rete neurale completamente connessa
2. Usa lo strumento grafico per progettare la rete neurale
3. La "funzione di attivazione" del livello di output
Come addestrare una rete neurale
1. Algoritmo e principio di apprendimento
2. Costruisci e addestra reti neurali da zero
3. Riscrivi il codice usando PyTorch
4. Usa lo strumento grafico per addestrare la rete neurale
Alcuni importanti problemi della rete neurale
1. Struttura di rete
2. sovradattamento
3. inadeguato
4. Overfitting vs underfitting
5. Inizializzazione
6. Gradiente che svanisce e gradiente che esplode
Rete neurale convoluzionale (CNN)
1. 1D-convoluzione
2. Esperimenti di convoluzione 1D
3. 1D-raggruppamento
4. Esperimenti 1D-CNN
5. 2D-CNN
6. Esperimenti 2D-CNN
Rete neurale ricorrente (RNN)
1. Vanilla RNN
2. Seq2seq, Autoencoder, Encoder-Decoder
3. RNN avanzato
4. Esperimento di classificazione RNN
Elaborazione del linguaggio naturale
1. Embedding: converti simboli in valori
2. Classificazione testo 1
3. Classificazione testo 2
4. TextCNN
5. Riconoscimento di entità
6. Segmentazione delle parole, tag e suddivisione in parti del discorso
7. Tag di sequenza in azione
8. RNN Bi bidirezionale
9. BI-LSTM-CRF
10. Attenzione
Modelli di linguaggio
1. Modello n-gram: Unigram
2. Modello n-gram: Bigram
3. Modello n-gram: Trigram
4. Modello RNN
5. Modello Transformer
Algebra lineare
1. Vettore
2. Matrice
3. Immergiti nella moltiplicazione di matrici
4. Tensore

Cos'è la rete neurale?

Panoramica

In breve, la rete neurale è una funzione: dati di input, risultato di output.

Funzione

Prendiamo come esempio il riconoscimento dell'immagine di cifre scritte a mano MNIST per definire il modulo della funzione corrispondente:

Tipo di attività: Classificazione delle immagini
Input: un'immagine contiene 28 x 28=784 pixel e ogni pixel è rappresentato da un numero reale
Uscita: 0-9
Descrizione attività: identifica il numero univoco dall'immagine
Definizione funzione

\begin{aligned} y &= f(x_1, x_2, ..., x_{784}) \\ &x_i \in \mathbb R, i = 1, ..., 784 \\ &y \in \{0, 1, ..., 9\} \end{aligned}

Questa è un'applicazione entry-level di Neural Network. L'input è un'immagine in scala di grigi a bassa risoluzione (28 x 28), corrispondente a una funzione con 784 variabili di input. Se si tratta di un'immagine a colori megapixel, le variabili di input corrispondenti raggiungeranno i 3 milioni.

Si può vedere che la rete neurale viene utilizzata per risolvere alcuni problemi complessi e anche le funzioni corrispondenti sono complesse. La realizzazione dell'algoritmo consiste nel costruire la funzione corrispondente.

Come costruire una funzione così complicata? Possiamo iniziare con semplici funzioni. L'esempio più semplice e di maggior successo sono i circuiti digitali.

Circuiti digitali

I circuiti digitali sono le pietre miliari dei computer e hanno costruito il nostro enorme mondo digitale. Ma il suo nucleo è composto da porte logiche AND, OR e NOT.

Cos'è una porta logica? In realtà è una funzione. E sono le funzioni più semplici.

Porta logica	espressione	forma funzione
AND cancello	$x \land y$	$z = \land(x, y)$
OR cancello	$x \lor y$	$z = \lor(x, y)$
NOT cancello	$\lnot x$	$y = \lnot(x)$

Tipo variabile: tutte le variabili booleane, solo 2 valori: $\{T, F\}$ , molto più semplici dei numeri naturali ( $\mathbb N$ ) e dei numeri reali ( $\mathbb R$ ).
Numero di variabili: funzione unaria o binaria, che è anche la forma più semplice di funzione
Rappresentazione della funzione: usa la tabella di verità per la descrizione. Perché non usare le immagini? Poiché è una funzione discreta, ci sono alcuni punti isolati sull'immagine, che non sono molto attraenti.

NOT cancello

$x$	$\lnot x$
$T$	$F$
$F$	$T$

NOT immagine gate (usa 0 per $F$ e 1 per $T$ )

AND cancello、OR cancello

$x$	$y$	$x \land y$	$x \lor y$
$T$	$T$	$T$	$T$
$T$	$F$	$F$	$T$
$F$	$T$	$F$	$T$
$F$	$F$	$F$	$F$

AND immagine porta

OR immagine porta

Porta logica combinata

Combina semplici porte logiche per ottenere funzioni più potenti.

Costruisci una nuova funzione binaria:

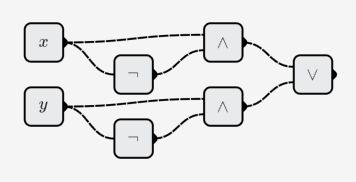
XOR: $x \oplus y = (x \land \lnot y) \lor (\lnot x \land y)$

XNOR: $x \odot y = (x \land y) \lor (\lnot x \land \lnot y)$

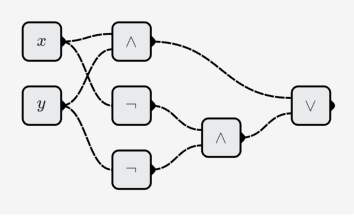
Costruisci una funzione multivariata:

Operazione AND a 3 bit: $f(x, y, z) = x \land y \land z$

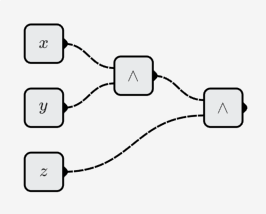
sommatore a 8 bit: $f(x_1, ..., x_8, y_1, ..., y_8)$ $f (x_{1}, ..., x_{8}, y_{1}, ..., y_{8})$
- È una funzione a 16 elementi contenente 16 variabili booleane
sommatore a 32 bit: $f(x*1, ..., x*{32}, y*1, ..., y*{32})$ $f (x * 1, ..., x * 32, y * 1, ..., y * 32)$
- È una funzione a 64 elementi contenente 64 variabili booleane
- Può anche essere considerato come una funzione binaria di interi a 32 bit: $f(x, y) \quad x, y \in \text{Int32}$

Ricapitolare

Combinando semplici funzioni di porta logica, è possibile costruire nuove funzioni logiche. Comprese operazioni come addizione, sottrazione, moltiplicazione e divisione di numeri interi a 32 bit e operazioni di tipi a virgola mobile a precisione singola a 32 bit, ecc.

Linguaggio di programmazione

Diamo un'occhiata di nuovo ai linguaggi di programmazione. Prendi Python come esempio, guarda gli elementi in Python.

Operatore

Nome	Simbolo	Funzione
Operatori logici	and or not	Funzioni logiche binarie e unarie
Operatori aritmetici	+, -, , /, %, *, //	Funzioni binarie
Operatori di confronto	==, !=, >, <, >=, <=	Funzioni binarie
...

Prendendo come esempio l'operatore di addizione di numeri in virgola mobile (+), l'immagine della funzione è la seguente:

$f(x, y) = x + y$

Funzioni

Puoi definire le tue funzioni in Python:

def f(x, y):
    return max(0, 2*x + 3*y - 3)

Qui viene definita una nuova funzione. Usa "+, -, *, max" e altre funzioni per costruire la nuova funzione. Il metodo di costruzione passa anche attraverso la composizione delle funzioni.

Ricapitolare

Le funzioni sono ovunque nei linguaggi di programmazione. Combinando le funzioni di base, si possono costruire nuove funzioni e si possono ottenere nuovi algoritmi.

Rete neurale

La rete neurale è anche funzione. Come i circuiti digitali e i linguaggi di programmazione, è composto anche da semplici funzioni. Le unità di base dei circuiti digitali sono funzioni logiche come AND, OR e NOT. Le unità di base nei linguaggi di programmazione sono funzioni come vari operatori, mentre l'unità di base delle reti neurali sono i neuroni.

Neurone

Allora cos'è un neurone? Un neurone biologico è una cellula con dendriti di input e assoni di output. E il neurone sulla rete neurale è un neurone artificiale, è anche una funzione, più precisamente, è una specie di funzione.

Il numero di input dei neuroni può essere modificato, il che significa che rappresenta una funzione dell'elemento $n$ $f(x_1, ..., x_n)$ e $n$ può essere diverso per diversi neuroni.

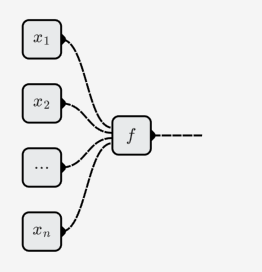
Rete neurale

I neuroni si combinano tra loro per formare una rete neurale. Come mostrato di seguito:

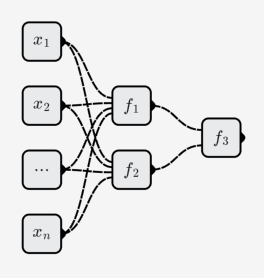
La rete neurale contiene tre neuroni (non contare i neuroni di input):

$f_1(x_1, ..., x_n)$
$f_2(x_1, ..., x_n)$
$f_3(x_1, x_2)$

La funzione rappresentata dalla rete neurale è:

f(x_1, ..., x_n) = f_3(f_1(x_1, ..., x_n), f_2(x_1, ..., x_n))

Ricapitolare

Il nucleo dei circuiti digitali (hardware) è la funzione e le sue funzioni di base sono le funzioni della porta logica AND OR NOT;
Il nucleo dei linguaggi di programmazione (software) è la funzione e le sue funzioni di base sono varie funzioni dell'operatore e funzioni integrate (fornite dall'hardware o composte);
Il nucleo delle reti neurali è anche la funzione e le sue funzioni di base sono i neuroni;
Nuove funzioni possono essere costruite attraverso la composizione di semplici funzioni. Le reti neurali sono funzioni costruite da funzioni neuronali attraverso operazioni di composizione di funzioni.

Domanda

Qual è esattamente la funzione rappresentata da un neurone?

Il solo sapere che si tratta di una funzione di elemento $n$ non è sufficiente. Le unità di base AND, OR e NOT nei circuiti digitali elencano tutte la tabella della verità e disegnano la figura, ma per quanto riguarda il neurone?